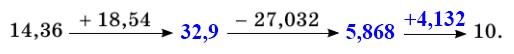Мерзляк 5 класс — § 33. Сложение и вычитание десятичных дробей

Опубликовано 15.06.202028.03.2022 автором mmetalnik

Ответы к учебнику для 5 класса. А. Г. Мерзляк

Переход на главную страницу сайта

Вопросы к параграфу

1. Сформулируйте правило сложения десятичных дробей.

Чтобы сложить две десятичные дроби, надо:

уравнять слагаемые в количестве цифр после запятой;
записать слагаемые друг под другом так, чтобы каждый разряд второго слагаемого оказался под соответствующим разрядом первого слагаемого;
сложить полученные числа так, как складывают натуральные числа;
поставить в полученной сумме запятую под запятыми в слагаемых.

2. Сформулируйте правило вычитания десятичных дробей.

Чтобы из одной десятичной дроби вычесть другую, надо:

уравнять в уменьшаемом и вычитаемом количестве цифр после запятой;
записать уменьшаемое и вычитаемое так, чтобы каждый разряд вычитаемого оказался под соответствующим разрядом уменьшаемого;
произвести вычитание так, как вычитают натуральные числа;
поставить в полученной разности запятую под запятыми в уменьшаемом и вычитаемом.

Решаем устно

1. Какая из следующих десятичных дробей равна дроби $\frac{79}{100000}$ .

0,79000
0,0079
0,00079 — десятичная дробь, равная заданной
0,7900

2. Какая из следующих десятичных дробей наибольшая:

43,56
43,561 — наибольшая десятичная дробь
43,559
43,55

3. Какое из следующих чисел получим, если округлим десятичную дробь 6,27 до десятых:

6,2
6,3 — округлённая до десятых десятичная дробь 6,27
6,26
6,28

4. На двух полках вместе на 20 книг больше, чем на каждой из них. Сколько книг на каждой полке?

Из условия следует, что:

на первой полке книг на 20 меньше, чем на обеих полках вместе, то есть на второй полке находится 20 книг;
на второй полке книг на 20 меньше, чем на обеих полках вместе, то есть на первой полке находится 20 книг.

Ответ: на каждой из полок по 20 книг.

5. Сравните:

1) 2 м = 200 см

2) 20 см = 0,2 м.

Упражнения

863. Вычислите:

864. Выполните сложение:

865. Выполните сложение:

866. Выполните вычитание:

867. Выполните вычитание:

868. Решите уравнение:

869. Решите уравнение:

870. В декабре фермер получил прибыль в размере 438,86 тысячи рублей, а в январе — на 16,4 тысячи рублей больше, чем в декабре. Сколько тысяч рублей составила прибыль фермера за декабрь и январь вместе?

1) 438,86 + 16,4 = 455,26 (тыс. р.) — прибыль фермера в январе.

2) 438,86 + 455,26 = 894, 12 (тыс. р.) — прибыль фермера за январь и февраль.

Ответ: 894,12 тыс. рублей.

871. Баба-яга купила новую двухкомнатную избушку на курьих ножках. Площадь одной комнаты составляет 17,6 м², что на 5,9 м² меньше, чем площадь второй. Вычислите для Бабы-яги общую площадь двух её комнат.

1) 17,6 + 5,9 = 23,5 (м²) — площадь второй комнаты.

2) 17,6 + 23,5 = 41,1 (м²) — площадь двух комнат.

Ответ: 41,4 м².

872. Собственная скорость теплохода равна 23,8 км/ч, скорость течения реки — 1,6 км/ч. Найдите скорость теплохода против течения и его скорость по течению реки.

1) 23,8 + 1,6 = 25,4 (км/ч) — скорость теплохода по течению реки.

2) 23,8 — 1,6 = 22, 2 (км/ч) — скорость теплохода против течения реки.

Ответ: по течению реки 25,4 км/ч, а против течения реки 22,2 км/ч.

873. Собственная скорость моторной лодки равна 16,4 км/ч, скорость течения — 1,8 км/ч. Найдите скорость лодки по течению и её скорость против течения реки.

1) 16,4 + 1,8 = 18,2 (км/ч) — скорость лодки по течению реки.

2) 16,4 — 1,8 = 14,6 (км/ч) — скорость лодки против течения реки.

Ответ: по течению реки 18,2 км/ч, а против течения реки 14,6 км/ч.

874. Скорость катера по течению реки равна 30,2 км/ч, а скорость течения — 2,2 км/ч. Найдите собственную скорость катера и его скорость против течения.

1) 30,2 — 2,2 = 28 (км/ч) — собственная скорость катера.

2) 28 — 2,2 = 25, 8 (км/ч) — скорость катера против течения.

Ответ: собственная скорость катера 28 км/ч, а скорость катера против течения — 25,8 км/ч.

875. Скорость катера на подводных крыльях против течения реки равна 68,5 км/ч, а скорость течения — 1,5 км/ч. Найдите собственную скорость катера и его скорость по течению.

1) 68,5 + 1,5 = 70 (км/ч) — собственная скорость катера на подводных крыльях.

2) 70 + 1,5 = 71,5 (км/ч) — скорость катера на подводных крыльях по течению реки.

Ответ: собственная скорость — 70 км/ч, скорость по течению реки — 71,5 км/ч.

876. Скорость лодки против течения реки равна 18,8 км/ч, а её собственная скорость — 20,2 км/ч. Найдите скорость течения и скорость лодки по течению реки.

1) 20,2 — 18,8 = 1,4 (км/ч) — скорость течения реки.

2) 20,2 + 1,4 = 21,6 (км/ч) — скорость движение лодки по течению реки.

Ответ: скорость течения реки — 1,4 км/ч, а скорость движения по течению — 21,6 км/ч.

877. Скорость катера по течению реки равна 32,6 км/ч, а его собственная скорость — 30,4 км/ч. Найдите скорость течения и скорость катера против течения реки.

1) 32,6 — 30,4 = 2,2 (км/ч) — скорость течения реки.

2) 30,4 — 2,2 = 28, 2 (км/ч) — скорость движения против течения.

Ответ: скорость течения реки — 2,2 км/ч, а скорость движения против течения — 28,2 км/ч.

878. Лена и Оля собрали вместе 3,2 кг грибов, причём Лена собрала 1,68 кг. Кто из девочек собрал больше грибов и на сколько килограммов?

1) 3,2 — 1,68 = 1,52 (кг) — грибов собрала Оля.

2) 1,68 > 1,52 — значит Лена собрала грибов больше, чем Оля.

3) 1,68 — 1,52 = 0,16 (кг) — грибов Лена собрала больше, чем Оля.

Ответ: Лена собрала на 0,16 кг грибов больше, чем Оля.

879. В первый день туристы прошли 6,3 км, что на 2,84 км меньше, чем во второй день. После двух дней похода им осталось пройти ещё 14,35 км. Какова протяжённость туристского маршрута?

1) 6,3 + 2,84 = 9,14 (км) — прошли туристы во второй день.

2) 6,3 + 9,14 = 15,44 (км) — прошли туристы в первые два дня.

3) 15,44 + 14,35 = 29,79 (км) — протяжённость маршрута.

Ответ: 29,79 км.

880. За первую неделю магазин продал 2,16 т картофеля, а за вторую — на 0,976 т больше, чем за первую. После этого в магазине ещё осталось 3,58 т картофеля. Сколько тонн картофеля было завезено в магазин?

1) 2,16 + 0,976 = 3,136 (т) — картофеля продали за вторую неделю.

2) 2,16 + 3,136 = 5, 296 (т) — картофеля продали за две недели.

3) 5,296 + 3,580 = 8,876 (т) — картофеля было завезено в магазин.

Ответ: 8,876 т.

881. Найдите общую площадь пустынь на поверхности земного шара, если площадь пустынь в Австралии равна 0,4 млн км², в Америке — на 1,2 млн км² больше, чем в Австралии, в Азии — на 1,4 млн км² больше, чем в Америке, а в Африке — на 2,8 млн км² больше, чем в Америке.

1) 0,4 + 1,2 = 1,6 (млн км²) — площадь пустынь в Америке.

2) 1,6 + 1,4 = 3 (млн км²) — площадь пустынь в Азии.

3) 1,6 + 2,8 = 4,4 (млн км²) — площадь пустынь в Африке.

4) 0,4 + 1,6 + 3 + 4,4 = 2 + 3 + 4,4 = 5 + 4,4 = 9,4 (млн км²) — общая площадь пустынь.

Ответ: 9,4 млн км².

882. Наибольшее озеро в мире — Каспийское море — имеет глубину 1,025 км. Озеро Байкал — самое глубокое в мире. Его глубина на 0,515 км больше глубины Каспийского моря. Глубина озера Танганьика (Африка) составляет 1,47 км. На сколько Байкал глубже Танганьики, а Танганьика глубже Каспийского моря?

1) 1,025 + 0,515 = 1,540 (км) — глубина озера Байкал.

2) 1,470 — 1,025 = 0,445 (км) — озеро Танганьика глубже Каспийского моря.

3) 1,54 — 1,47 = 0,07 (км) — озеро Байкал глубже озера Танганьика.

Ответ: Байкал глубже Танганьики на 0,007 км, а Танганьика глубже Каспийского моря на 0,445 км.

883. Отправившись на ядре в путешествие на Луну, барон Мюнхгаузен в первую минуту пролетел 234,7 км, что на 18,6 км меньше, чем во вторую минуту. В третью минуту он пролетел на 156,4 км меньше, чем в первую и вторую минуты вместе. Сколько километров пролетел Мюнхгаузен за первые три минуты полёта?

1) 234,7 + 18,6 = 253,3 (км) — пролетел за вторую минуту.

2) 234,7 + 253,3 = 488 (км) — пролетел за первые две минуты.

3) 488 — 156,4 = 331,6 (км) — пролетел за третью минуту.

4) 488 + 331,6 = 819,6 (км) — пролетел за первые три минуты.

Ответ: 819,6 км.

884. В понедельник в столовой израсходовали 12,4 кг сахара, что на 2,8 кг больше, чем во вторник. В среду сахара было израсходовано на 5,6 кг меньше, чем в понедельник и во вторник вместе. Сколько всего килограммов сахара израсходовали в понедельник, вторник и среду?

1) 12,4 — 2,8 = 9,6 (кг) — сахара израсходовали во вторник.

2) 12,4 + 9,6 = 22 (кг) — сахара израсходовали в понедельник и вторник.

3) 22 — 5,6 = 16,4 (кг) — сахара израсходовали в среду.

4) 22 + 16,4 = 38,4 (кг) — сахара израсходовали в понедельник, вторник и среду.

Ответ: 38,4 кг.

885. За три дня на шахте добыли 2 436,86 т угля. За первый день добыча составляла 827,48 т, а за второй — на 59,59 т меньше, чем за первый. Сколько тонн угля добыли за третий день?

1) 827,48 — 59,59 = 767,89 (т) — угля добыли во второй день.

2) 827,48 + 767,89 = 1 595,37 (т) — угля добыли в первые два дня.

3) 2 436,86 — 1 595,37 = 841,49 (т) — угля добыли в третий день.

Ответ: 841,49 т.

886. Фермер Василий Работящий взял в аренду три участка земли общей площадью 3 428,32 га. Площадь одного из этих участков была равна 1 506,46 га, что на 237,64 га меньше площади второго участка. Найдите площадь третьего участка.

1) 1 506,46 + 237,64 = 1 744,10 (га) — площадь второго участка.

2) 1 506,46 + 1 744,10 = 3 250,56 (га) — площадь первого и второго участка вместе.

3) 3 428,32 — 3 250,56 = 177,76 (га) — площадь третьего участка.

Ответ: 177,76 га.

887. Ломаная состоит из трёх звеньев. Длина первого звена 9,2 см, что на 3,5 см больше длины второго звена и на 4,9 см меньше длины третьего. Найдите длину ломаной.

1) 9,2 — 3,5 = 5,7 (см) — длина второго звена.

2) 9,2 + 4,9 = 14,1 (см) — длина третьего звена.

3) 9,2 + 5,7 + 14,1 = 29 (см) — длина ломаной.

Ответ: 29 см.

888. Одна из сторон треугольника равна 12,4 дм, что на 3,8 дм меньше второй стороны и на 2,6 дм больше третьей. Вычислите периметр треугольника.

1) 12,4 + 3,8 = 16,2 (дм) — длина второй стороны треугольника.

2) 12,4 — 2,6 = 9,8 (дм) — длина третьей стороны треугольника.

3) 12,4 + 16,2 + 9,8 = 38,4 (дм) — периметр треугольника.

Ответ: 38,4 дм.

889. Найдите значение выражения:

890. Найдите значение выражения:

891. Решите уравнение:

892. Решите уравнение:

893. Выполните сложение, выбирая удобный порядок вычислений:

1) (2,45 + 0,276) + 4,55 = (2,45 + 4,55) + 0,276 = 7 + 0, 276 = 7,276

2) (9,37 + 13,6) + 6,4 = 9,37 + (13,6 + 6,4) = 9,37 + 20 = 29,37

3) 5,12 + 3,75 + 5,25 + 4,88 = (3,75 + 5,25) + (5,12 + 4,88) = 9 + 10 = 19

4) 0,234 + 0,631 + 0,766 + 0,369 = (0,234 + 0,766) + (0,631 + 0,369) = 1 + 1 = 2

894. Выполните сложение, выбирая удобный порядок вычислений:

1) (12,82 + 8,394) + 5,18 = (12,82 + 5,18) + 8,394 = 18 + 8,394 = 26,394

2) 2,53 + 15,1 + 4,47 + 14,9 = (2,53 + 4,47) + (15,1 + 14,9) = 7 + 30 = 37

895. Упростите выражение:

1) 2,46 + а + 81,139 + 14,8 = ( 2,46 + 81,139 + 14,8) + а = 98,399 + а

2) m + 0,47 + 5,062 + m + 43,295 = (m + m) + (0,47 + 5,062 + 43,295) = 2m + 48.827

3) х + 0,3 + 0,9007 + 4,58 + 3x = (x + 3x) + (0,3 + 0,9007 + 4,58 ) = 4x + 5,7807

4) 7c + 236,7 + 2c + 0,82 + 4,325 = (7c + 2c) + (236,7 + 0,82 + 4,325) = 9c + 241,845

896. Найдите числа, которых не хватает в цепочке вычислений:

a = 14,36 + 18,54 = 32,9

b = 32,9 — 27,032 = 5,868

x = 10 — 5,868 = 4,132

897. Найдите числа, которых не хватает в цепочке вычислений:

a = 39,8 — 14,48 = 25,32

x = 74,123 — 25,32 = 48,803

y = 74,123 — 40,2 = 33,923

898. Вместо звёздочек поставьте цифры так, чтобы сложение (вычитание) было выполнено верно:

899. Как изменится сумма, если:

1) одно из слагаемых увеличить на 6,8, а второе — на 4,25

6,8 + 4,25 = 11,05 — сумма увеличится на 11,5.

2) одно из слагаемых увеличить на 14,3, а второе уменьшить на 7,15

14,3 — 7,15 = 7,15 — сумма увеличится на 7,15.

3) одно из слагаемых увеличить на 3,2, а второе уменьшить на 3,2?

3,2 — 3,2 = 0 — сумма не изменится.

900. Как изменится разность, если:

1) уменьшаемое увеличить на 9,25

разность увеличится на 9,25

2) уменьшаемое уменьшить на 7,6

разность уменьшится на 7,6

3) вычитаемое увеличить на 12,2

разность уменьшится на 12,2

4) вычитаемое уменьшить на 17,96

разность увеличится на 17,96

5) уменьшаемое увеличить на 0,4, а вычитаемое — на 0,3

0,4 — 0,3 = 0,1 — разность увеличится на 0,1

6) уменьшаемое увеличить на 2,3, а вычитаемое уменьшить на 1,7

2,3 + 1,7 = 4 — разность увеличится на 4

7) уменьшаемое уменьшить на 6,1, а вычитаемое увеличить на 3,4

6,1 + 3,4 = 9,5 разность уменьшится на 9,5

901. Выразите данные величины в дециметрах и выполните действия:

1) 2,34 дм — 18 см = 2,34 дм — 1,8 дм = 0,54 дм

2) 9,6 дм + 4 см = 9,6 дм + 0,4 дм = 10 дм

3) 49 дм — 324 см 49 дм — 32,4 дм = 16,6 дм

4) 5,63 м + 2 345 см = 56,3 дм + 234,5 дм = 290,8 дм

5) 9 м 8 дм 3 см — 25 см 8 мм = 98,3 дм — 2,58 дм = 95,72 дм

6) 1 м 5 дм 6 см — 16 см 9 мм = 15,6 дм — 1,69 дм = 13,91 дм

902. Выразите данные величины в арах и выполните действия:

1) 3 а 82 м² + 8 а 9 м² = 3,52 а + 8,09 а = 11,91 а

2) 28 а 7 м² + 14 а 26 м² =28,07 а + 14,26 а = 42,33 а

3) 57 а 22 м² — 48 а 4 м² = 57,22 а + 48,04 а = 10526 а

4) 41 а 5 м² — 36 а 19 м² = 4105 а — 36,19 а = 4,86 а

5) 9 га 6 а 8 м² + 18 а 10 м² = 906,08 а + 18,10 а = 924,18 а

6) 24 га 8 а 4 м² — 24 а 20 м² = 2408,04 а — 24,2 а = 2383,84 а

903. Выразите данные величины в центнерах и выполните действия:

1) 9 ц — 524 кг = 9 ц — 5,24 ц = 3,76 ц

2) 8 ц 44 кг — 836 кг = 8,44 ц — 8,36 ц = 0,08 ц

3) 42 ц 5 кг + 85 кг = 45,05 ц + 0,85 ц = 42,9 ц

4) 2,92 т + 684 кг = 29,2 ц + 6,84 ц = 36,04 ц

5) 7 т 6 ц 4 кг — 8 ц 18 кг = 7604 ц — 8,18 ц = 67,86 ц

6) 1 т 2 ц 3 кг — 1 т 15 кг = 12,03 ц — 10,15 ц = 1,88 ц

904. Найдите значение выражения, выбирая удобный порядок вычислений:

1) (4,12 + 0,116) — 1,12 = (4,12 — 1,12) + 0,116 = 3 + 0,116 = 3,116

2) (5,93 + 67,5) — 27,5 = 5,93 + (67,5 — 27,5) = 5,93 + 40 = 45,93

3) 0,844 — (0,244 + 0,018) = (0,844 — 0,244) — 0,018 = 0,600 — 0,018 = 0, 582

4) 7,29 — (3,961 + 2,29) = (7,29 — 2,29) — 3,961 = 5,000 — 3,961 = 1,039

Упражнения для повторения

905. От двух пристаней, расстояние между которыми равно 24 км, одновременно в одном направлении отчалили лодка и катер (лодка двигалась впереди катера). Скорость лодки равна 8 км/ч и составляет $\frac{4}{5}$ скорости катера. Через сколько часов после начала движения катер догонит лодку?

1) 8 : 4 • 5 = 2 • 5 = 10 (км/ч) — скорость катера.

2) 10 — 8 = 2 (км/ч) — скорость сближения катера и лодки.

3) 24 : 2 = 12 (ч) — катер догонит лодку.

Ответ: через 12 часов.

906. Длина бассейна равна 12 м, ширина его составляет $\frac{3}{4}$ длины, а глубина — $\frac{2}{3}$ ширины. Водой было наполнено $\frac{11}{18}$ объёма бассейна. Сколько кубических метров воды налили в бассейн?

1) 12 : 4 • 3 = 3 • 3 = 9 (м) — ширина бассейна.

2) 9 : 3 • 2 = 3 • 2 = 6 (м) — глубина бассейна.

3) 12 • 9 • 6 = 108 • 6 = 648 (м³) — объем бассейна.

4) 648 : 18 • 11 = 36 • 11 = 396 (м³) — наполнено.

Ответ: 396 м³.

907. За шоколадку и четыре пирожных заплатили 414 р., а за такую же шоколадку и восемь таких пирожных — 750 р. Сколько рублей стоит шоколадка?

1) 750 — 414 = 336 (рублей) — стоят 4 пирожка, так как вторая покупка отличается от первой именно на 4 пирожка.

2) 414 — 336 = 78 (рублей) — стоит шоколадка, так как в первую покупку купили 1 шоколадку и 4 пирожка.

Ответ: 78 рублей.

Задача от мудрой совы

908. Хитрый Лисёнок предложил Петру Скупердяйкину: «Каждый раз, когда ты перейдёшь мост, который я заколдую, твои деньги удвоятся. За это будешь мне каждый раз отдавать 24 монеты».

Сделал Скупердяйкин так три раза и остался совсем без денег.

Сколько денег было у Петра до встречи с Хитрым Лисёнком?

1 способ — при помощи уравнения

Пусть х монет было у Скупердяйкина сначала. Тогда после перехода 1 моста стало (2х — 24) монет, после перехода второго моста стало ((2х — 24) • 2 — 24) монет, а после перехода третьего моста стало (((2х — 24) • 2 — 24) • 2 — 24) или 0 монет. Можем составить уравнение:

((2х — 24) • 2 — 24) • 2 — 24 = 0
((2х — 24) • 2 — 24) • 2 = 24
(2х — 24) • 2 — 24 = 24 : 2
(2х — 24) • 2 — 24 = 12
(2х — 24) • 2 = 12 + 24
(2х — 24) • 2 = 36
2х — 24 = 36 : 2
2х — 24 = 18
2х = 18 + 24
2х = 42
х = 42 : 2
х = 21 (монета) — была у Скупердяйкина вначале.

Ответ: 21 монета.

2 способ — от конца до начала

1) (0 + 24) : 2 = 24 : 2 = 12 (монет) — было до перехода через третий мост.

2) (12 + 24) : 2 = 36 : 2 = 18 (монет) — было до перехода через второй мост.

3) (18 + 24) : 2 = 42 : 2 = 21 (монета) — была до перехода через первый мост, то есть в самом начале.